|
 |
||||||||||||||
 |
|||||||||||||||
 |
 |
 |
 |
 |
|||||||||||
 |
 |
 |
|||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
 |
||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
 |
 |
||||||||||||||
 |
 |
||||||||||||||
 |
|||||||||||||||
 |
|||||||||||||||
Коворкинг 2.0
| ↑ наверх |
Коворкинг-центр Клуб НагатиноЧто это? Коворкинг-центр в Клубе Нагатино — самый уютный и дешевый коворкинг в Москве. Наши тарифы начинаются от 5000 рублей за одно рабочее место в месяц. Учитывая, большой набор бесплатных услуг, бесплатные семинары и мероприятия. Но и этого нам показалось мало и мы решили сделать вам Новогодний подарок: первым 50 резидентам, пришедшим 25 декабря 2012 года на открытие, мы готовы отдать рабочее место в хорошие руки за полцены на любой срок. То есть, например, два месяца работы вам обойдутся по цене одного. Однако сделать это можно будет только 25 декабря. Как бы мы хотели, чтобы воспользоваться нашим предложением смогли все, но увы, список ограничен. Что здесь будет? Первая очередь нашего коворкинга — 100 рабочих мест. Эргономичные интерьеры разработаны в мастерской Руслана Айдарова. Высокие потолки, панорамный вид на Москву, антресоли для работы отдельных команд-стартапов, изолированные переговорные комнаты, конференц-зал, который по вечерам становится кинотеатром. В прошлом индустриальное пространство превратилось в богатый и многогранный офис для независимых и молодых. Но это не все. Мы готовы предложить Вам уникальную услуги среди московских коворкинг-центров - собственный мини-хостел, душ и даже детскую комнату. И, разумеется, - самый вкусный бесплатный кофе из цельных зерен. |
| ↑ наверх |
Что такое коворкинг: 2:0?Это инициатива Департамента науки, промышленной политики и предпринимательства Москвы. Проект «Москва: Коворкинг 2.0» — это новые возможности для развития малого бизнеса города Москвы. Цель проекта — создание благоприятных условий для работы независимых профессионалов и для развития новых бизнесов в реальном секторе экономики. Даже шире - это первый в России опыт создания социально-культурных офисных центров нового формата для молодых специалистов. Коворкинги в России существуют уже несколько лет, однако, назвать этот проект окончательно успешным нельзя. В России первый коворкинг появился в Екатеринбурге. Санкт-Петербург стал вторым городом после Екатеринбурга, где открылся коворкинг-центр. Однако, спустя несколько месяцев проект пришлось закрыть. Такая же участь постигла и ряд других коворкинг-центров, появившихся в Санкт-Петербурге. Сейчас, по разным оценкам, в городе насчитывается от 15 до 20 коворкинг-центров. Проблемы закрывшихся проектов могли быть в том, что на самом деле фрилансерам нужен больше чем офис. Просто стул и стол - этого мало. Просто рабочей атмосферы - тоже. Нужен необычный офис, нестандартный креативный подход к его обустройству. Кроме того, возможно, были просчеты в выстраивании бизнес-модели первых коворкингов. Именно поэтому мы заявили о перезагрузке коворкингов в формате 2.0 - с участием города. Первый и главный принцип – в коворкинге нет закрепленных рабочих мест, их могут арендовать любые компании или частные лица на любой отрезок времени. Покупая рабочее место, резидент может рассчитывать на пакет услуг – секретаря, переговорные комнаты, телефон - в зависимости от уровня коворкинга. Задачи коворкинг-центра состоят в развитии инфраструктуры и сопутствующих сервисов, а также интеграции в программы поддержки малого бизнеса, которые реализует правительство Москвы. Такая форма организации труда позволяет получить максимум офиса за минимум денежных средств. На начальном этапе развития бизнеса это лучший способ сэкономить на офисных площадях. Что будет с проектом в перспективе? В плане московских властей - сделать московские коворкинги центрами, где благодаря синергетическому эффекту молодые специалистами сначала становятся из фрилансеров участниками стартапов, а потом создают полноценный бизнес. Так стимулируется развитие предпринимательства в городе. Второй важный момент — коворкинги станут местом не только работы, но и обучения — для наиболее распространенных специальностей среди резидентов коворкингов мы подготовим программу деловых мероприятий и обучающих семинаров. Одним из пилотных проектов в рамках формирования новой архитектуры города и освоения бывших промышленных зон станет создание крупнейшего в Москве коворкинг-центра «Клуб Нагатино» на Варшавском шоссе. С открытием второй очереди на 300 рабочих мест в коворкинг-центре Клуб нагатино он станет крупнейшим не только в Москве, но и в России. По плану, вторая очередь будет запущена в строй в первой половине 2013 года. Он расположится на третьем этаже в Клубе Нагатино и станет одним из самых инновационным с архитектурной точки зрения офисом. |
| ↑ наверх |
Наши партнерыПартнерами коворкинг-центр в организации мероприятий выступает лидер на рынке подбора персонала для IT-компаний — агентство «Itmozg», ведущее информационное агентство для специалистов в архитектуре и дизайне — ИА «Архитектор». Сеть коворкингов в Москве «Искусство Гармонии» — аренда кабинета психолога Подписывайтесь на инстаграм — @harmony_cabinet_rent |
| ↑ наверх |
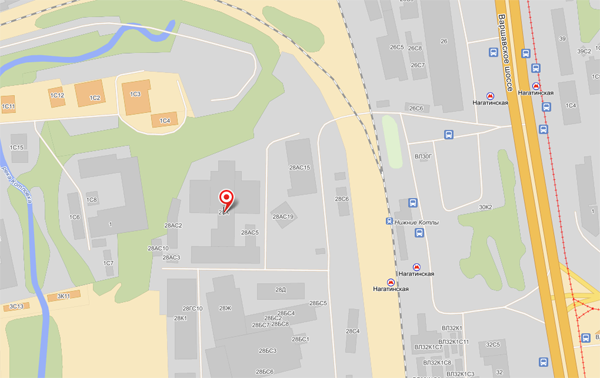
КонтактыАдрес: Москва, Варшавское шоссе, д. 28 А На машине (5 минут от Третьего Транспортного Кольца): Съезд с ТТК на Варшавское шоссе из центра, через 2 км поворот направо на ж/д переезд у платформы Нижние Котлы. Сразу за переездом находится шлагбаум, ограничивающий въезд на территорию Клуба Нагатино. На общественном транспорте (3 минуты от метро, 15 минут от Кремля): Метро Нагатинская, первый вагон из центра, выход к электропоездам. Поднимаетесь на улицу идете прямо 100 метров, пока не увидите слева переход через железную дорогу. Перейдите по нему и увидите шлагбаум. За шлагбаумом находится главный вход в Клуб Нагатино.
Отправить сообщение: Поля отмеченные*, обязательны для заполенения. |